Introduction: From Mathematical Theory to Cutting-Edge Innovation
In Part 1, we explored how linear algebra serves as the foundation for vectors, matrices, and transformations; these are the building blocks of modern technology. However, understanding the basics is just part of the picture.
The true power of linear algebra lies in its uses. Behind every breakthrough in AI, technology trends for 2025, big data analytics, robotics, and cybersecurity, there are layers of vector and matrix operations.
Think of it this way: if linear algebra is the grammar of mathematics, then artificial intelligence, data science, and modern computing are the stories we create with it. From the recommendations you find on Netflix to self-driving cars that navigate traffic, linear algebra turns theory into innovation.
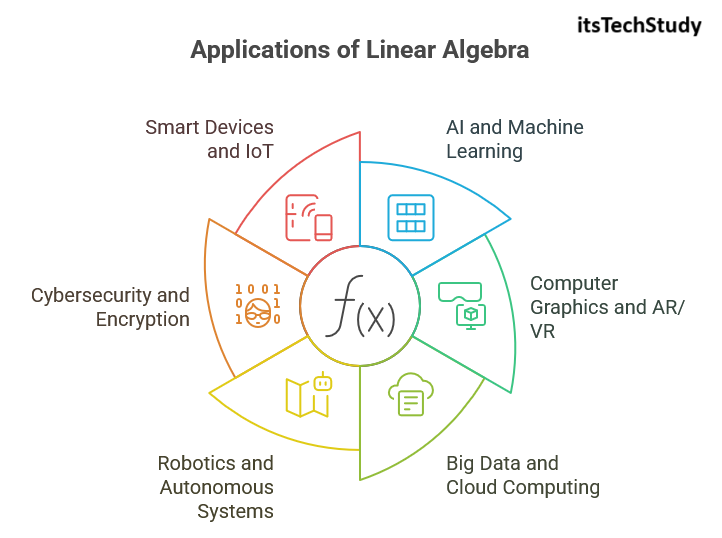
1. Linear Algebra in Artificial Intelligence (AI) and Machine Learning
AI and machine learning models depend on patterns within data. At its heart, data is organized in vectors and matrices.
Training neural networks: Each neuron is represented as a vector, and connections between them are kept in matrices. The learning process involves multiplying input vectors by weight matrices and adjusting them.
Image recognition: A photo is divided into pixel matrices. These matrices undergo transformations to identify edges, shapes, and eventually objects.
Natural language processing (NLP): Words and sentences are turned into vectors (called embeddings). Linear algebra operations compare these vectors to help chatbots, translators, and search engines understand meaning.
Example: When Google Translate changes text from English to Spanish, it relies on linear transformations of word vectors to relate meanings across languages.
2. Linear Algebra in Computer Graphics and AR/VR
Every 3D model, animation, or AR filter you see is backed by linear algebra.
Rotation matrices move objects smoothly in games and simulations.
Scaling matrices resize objects while keeping proportions intact.
Projection matrices let us see 3D objects on a 2D screen.
Example in AR/VR: When you try on virtual sunglasses using an AR app, the system uses transformations to match the digital frame with the precise position of your face in real-time.
3. Big Data and Cloud Computing
Data is growing rapidly, and managing it effectively requires matrix-based operations.
Data compression: Techniques such as Singular Value Decomposition (SVD) shrink vast datasets into smaller, meaningful forms.
Recommendation engines: These utilize matrix factorization to predict missing values, like your next favorite movie.
Parallel computing in the cloud: This breaks large matrix calculations into smaller tasks distributed across servers.
Table: Role of Linear Algebra in Data-Driven Industries
| Industry | Application | Example Use Case |
|---|---|---|
| Streaming Platforms | Recommendation systems (matrix factorization) | Netflix suggesting movies & shows |
| Finance | Risk modeling and portfolio optimization | Predicting stock movements with ML |
| Healthcare | Genomic data analysis | Finding disease patterns from DNA data |
| E-commerce | Personalization | Amazon suggesting products |
4. Robotics and Autonomous Systems
Robots and self-driving vehicles count on linear algebra for navigation, vision, and control systems.
Path planning: Vectors define directions and locations.
Sensor fusion: Matrix operations combine data from cameras, LIDAR, and GPS into a single model.
Control systems: Transformation matrices help robots adjust their movement in real-time.
Example: A self-driving car applies transformation matrices to read road signs, spot pedestrians, and figure out its path.
5. Cybersecurity and Encryption
Securing communication involves complex mathematical structures. Linear algebra is vital in cryptography.
Matrix-based ciphers encode and decode sensitive information.
Public key cryptography relies on transformations that are easy to perform but hard to reverse without the key.
Error correction: This is used in secure data transmission over the internet.
Example: When you log into your bank account, encryption methods supported by linear algebra keep your personal data safe from hackers.
6. Smart Devices and the Internet of Things (IoT)
From smart speakers to wearable health monitors, IoT devices use linear algebra to process signals and predictions.
Voice recognition: Audio waves become frequency vectors.
Health monitoring: Matrices keep track of data like heart rate, steps, and sleep patterns.
Energy efficiency: Linear algebra improves how resources are used across connected devices.
Pros and Cons of Relying on Linear Algebra in Tech
Pros
– Enables strong data-driven insights.
– Forms the backbone of AI and machine learning.
– Essential for computer graphics, AR/VR, and simulations.
– Provides effective tools for encryption and cybersecurity.
Cons
– High computational cost for large datasets.
– Can be mathematically challenging for beginners.
– Requires advanced optimization for real-time applications.
7. The Future of Linear Algebra: Quantum Computing and Beyond
As we look to the future, linear algebra will not just remain important; it will become even more essential.
Quantum computing: This uses vector spaces in complex dimensions to solve problems that traditional computers can’t handle.
AI advancements: More complex deep learning models rely on tensor operations, which are generalized matrices.
Next-gen simulations: From climate change models to virtual reality environments, matrix-based computations will grow in scope.
Example: In quantum computing, the state of a system is described as a vector in a complex space. Operations on this vector can solve tasks like cryptography or drug discovery much faster than classical systems.
Step-by-Step: How Linear Algebra Shapes Modern AI
1. Data Collection: Raw input like images, sounds, or text is gathered.
2. Vectorization: Inputs are changed into mathematical vectors.
3. Matrix Operations: Models apply filters, weights, and transformations.
4. Training Algorithms: Systems learn patterns by fine-tuning matrices.
5. Predictions & Actions: AI offers recommendations, recognitions, or real-world decisions.
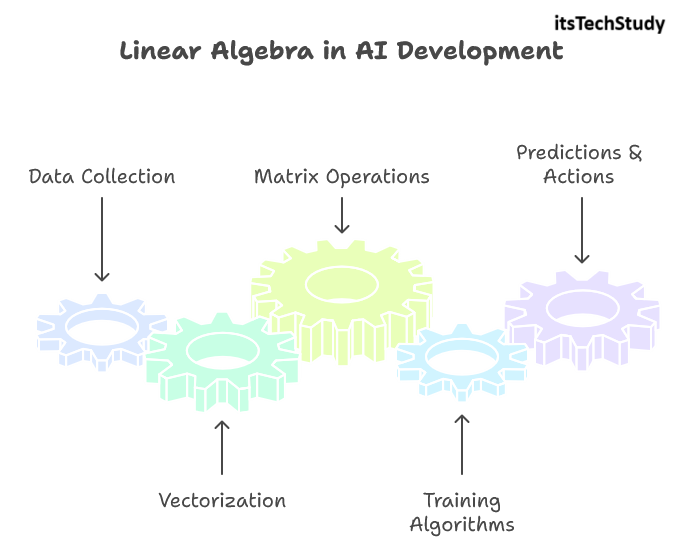
This cycle recurs in every AI system-from voice assistants to autonomous drones.
Conclusion: The Unshakable Role of Linear Algebra in Technology
From fueling AI recommendations and securing digital transactions to enabling self-driving vehicles and shaping the future of technology, linear algebra is the invisible force driving innovation.
We are entering a time when data is the new fuel, and linear algebra is the engine that processes it. Whether it’s cybersecurity tips, AI advancements, or the best tech gadgets of the future, every innovation returns to this mathematical foundation.
By mastering linear algebra, you’re not just learning equations-you’re gaining the key to unlocking tomorrow’s digital world.
Linear Algebra and the Future of Tech
Q1: Is linear algebra only useful for scientists and engineers?
Ans: No. With technology integrated into daily life, understanding linear algebra concepts helps everyone—from developers to business leaders—make informed decisions.
Q2: How is linear algebra used in AI chatbots and assistants?
Ans: Chatbots convert text into vectors, compare them mathematically, and generate responses using transformations.
Q3: Can I work in AI without mastering linear algebra?
Ans: Basic tools and frameworks hide the math, but for innovation and research, linear algebra knowledge is essential.
Q4: Will quantum computing replace classical linear algebra?
Ans: Not replace, but extend it. Quantum systems expand linear algebra into higher dimensions, making it even more powerful.
Q5: What’s the future demand for linear algebra skills in jobs?
Ans: Data science, machine learning, robotics, and cybersecurity roles all require strong linear algebra foundations. The demand is rising with every new tech innovation.












No Comments Yet
Be the first to share your thoughts.
Leave a Comment